YajinMo_Homework_2020/09/21
Task 01
请使用网页版的 blastp, 将上面的蛋白序列只与 mouse protein database 进行比对, 设置输出结果最多保留10个, E 值最大为 0.5。将操作过程和结果截图。
Y.Mo: 利用NCBI提供的在线Blast工具[1],对Target蛋白序列进行blastp分析 (Figure 1)。
>Target | Homework protein sequence for analysis
MSTRSVSSSSYRRMFGGPGTASRPSSSRSYVTTSTRTYSLGSALRPSTSRSLYASSPGGVYATRSSAVRL
分析步骤如下:
-
在blastp的query框中输入序列信息 (Figure 1A)
-
分别选择不同的查询数据库 (nr/refseq/swissprot)和物种 (mouse taxid: 10088)信息 (Figure 1C, D, E)
-
选择blast算法条件 (BLOSUM62, Max Target Sequence = 10, Expect threshold = 0.5) (Figure 1F)
-
Blast
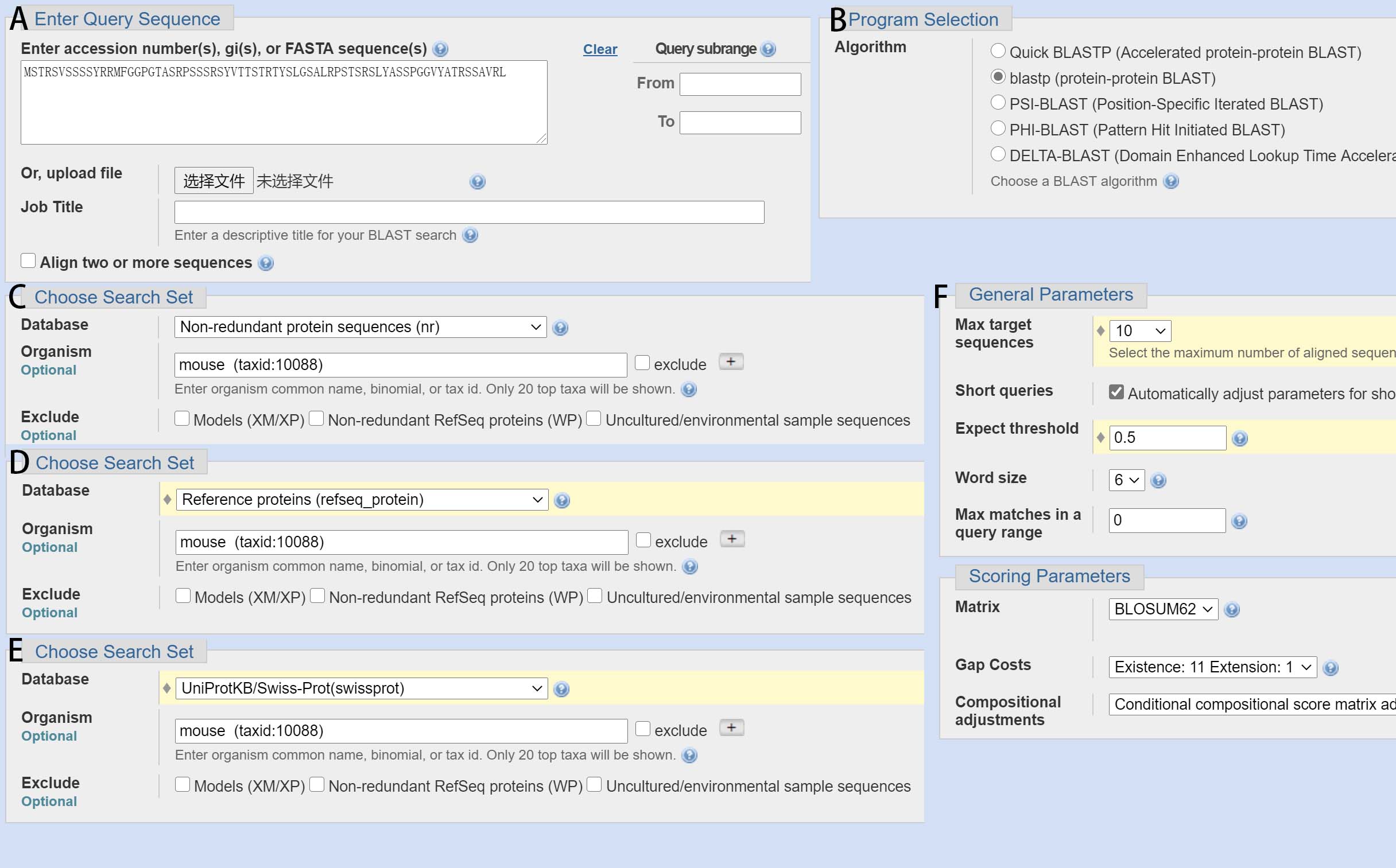 Figure 1. 使用NCBI在线Blast工具对目标蛋白序列进行blastp。A) 在query框输入目标蛋白序列,B) 选择blastp,C, D, E) 选择不同数据库中的小鼠比对,F) 更改算法中结果显示数量,E值大小以及打分矩阵。
Figure 1. 使用NCBI在线Blast工具对目标蛋白序列进行blastp。A) 在query框输入目标蛋白序列,B) 选择blastp,C, D, E) 选择不同数据库中的小鼠比对,F) 更改算法中结果显示数量,E值大小以及打分矩阵。
在全数据库(Non-redundant protein sequences, nr),RefSeq以及Swissprot中分别blast后,分别显示10条,2条和1条比对结果,其中RefSeq (Figure 2B)和Swissprot (Figure 2C)的结果对应的accession number都可以对应到nr (Figure 2A)中查到的结果。 另外,RefSeq中比对到的两条结果分别对应来自小鼠的两个不同种 Mus musculus (NP_035831.2)以及 Mus pahari (XP_021047825.1),但是Swissprot中仅比对出 Mus musculus 的对应蛋白序列 (P20152)。
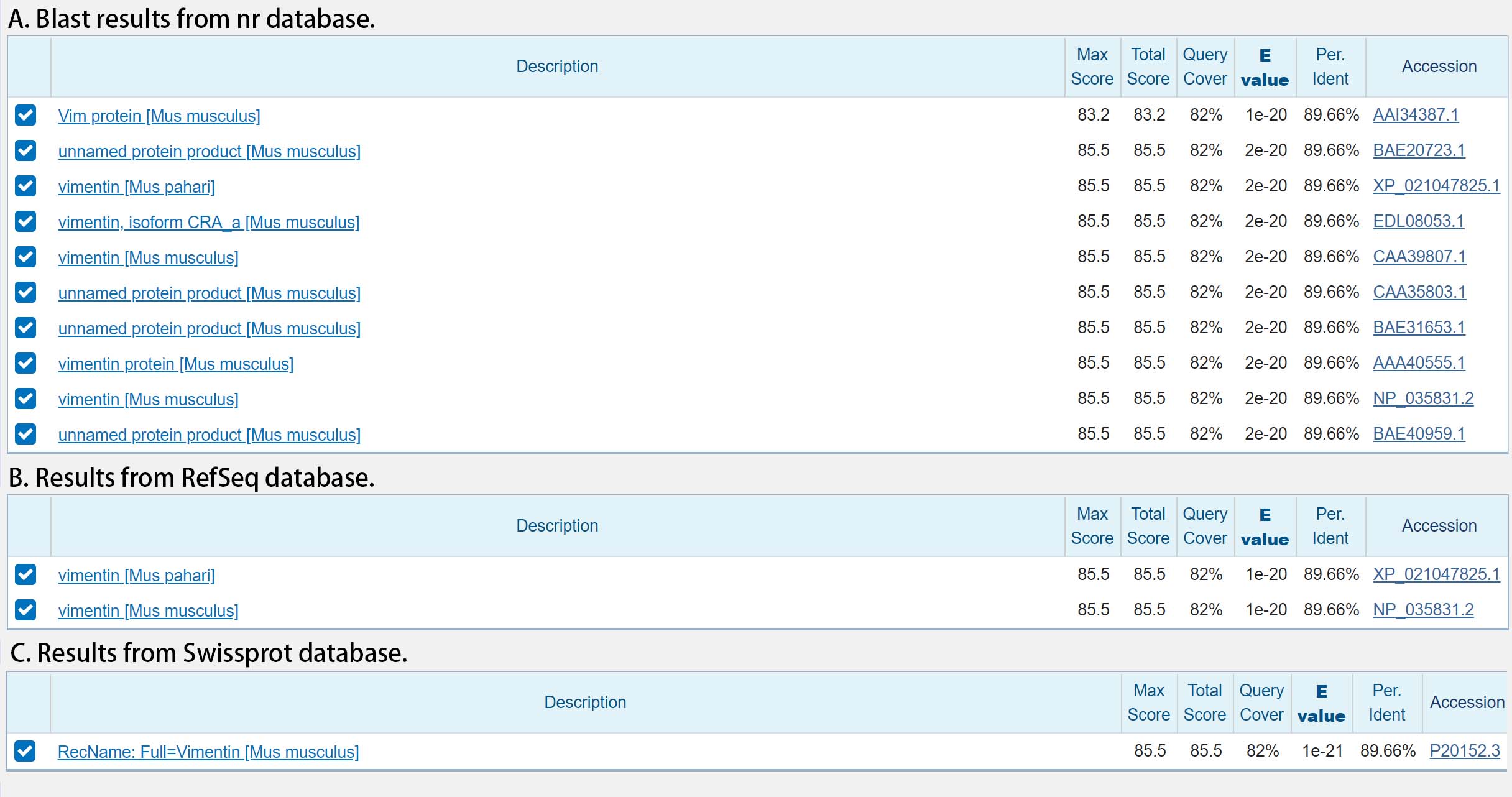 Figure 2. 使用NCBI在线Blast工具对目标蛋白序列在不同数据库中进行blastp后的结果。A) nr数据库中比对出10条结果,B) 从RefSeq数据库中比对出两条结果,C) Swissprot数据库中仅比对出一条蛋白序列
Figure 2. 使用NCBI在线Blast工具对目标蛋白序列在不同数据库中进行blastp后的结果。A) nr数据库中比对出10条结果,B) 从RefSeq数据库中比对出两条结果,C) Swissprot数据库中仅比对出一条蛋白序列
对于三种数据库选择对应不同的输出结果,nr的结果易于理解,因为从众多兼容数据库中提取序列信息,所以nr数据库可以blast出最多的结果。关键的不同是RefSeq和Swissprot的blast结果。
对比blast结果中的原序列,RefSeq的结果中来自两个小鼠种类的蛋白序列subject是相同的,但是在数据库中来自 Mus musculus 的序列是被令人信服的文献数据所注释的,但是来自 Mus pahari 的序列缺乏相应数量和质量的工作支持。并且,RefSeq也以不同的accession区别两条序列,来自 Mus musculus 的序列是NP,意味着和确定的mRNA以及DNA序列相关联,但是来自 Mus pahari 的序列是XP号,意味着蛋白的序列和结构甚至是对应的mRNA序列仅仅是预测性的。RefSeq在数据上更关注核酸数据的管理与注释,在蛋白序列的注释上没有专门的蛋白数据库那么详尽。Swissprot数据库更注重蛋白序列及其详尽的文献工作审查,所以目前主流的并具有详尽工作注释的小鼠种 Mus musculus 序列会在数据库中,而缺乏工作支持的 Mus pahari 没有在Swissprot中 (在Swissprot中的搜索经验中似乎没有发现过同属不同种的蛋白序列,每个属只有唯一蛋白序列序列?)。
Task 02 (Challenge Task)
总结和解释一下这两种(对称和不对称)PAM250不一样的原因及其在应用上的不同
Y.Mo: 非对称PAM矩阵更一般的代表PAM Mutation Probability Matrix M[i, j],Dayhoff统计了相似度 >= 85%的一个蛋白序列集后计算每个氨基酸i突变为其他氨基酸j的几率,并以此作为突变概率 M[i, j],也就是PAM1矩阵,自乘250次后得到相应的非对称PAM250矩阵,代表蛋白序列的位点在自然选择压力下发生250次1%的突变概率,目前的蛋白序列的比对从最末端节点到最初始节点的突变数被认为在250次以内,所以可以以此矩阵作为突变概率的参照。
在非对称PAM矩阵中,分数的分布能够反应两部分信息:
-
每个氨基酸分子结构的稳定性。以Cysteine为例,C能够在蛋白内形成二硫键,其键位结构稳定性对蛋白构象有重要影响,因此不容易突变为其他氨基酸,也对应了非对称PAM矩阵中的C-C对角值的高分数。
-
每个氨基酸分子的突变趋向和分子结构相似性。由非对称PAM分数,Alanine保持为Alanine和突变为Glycine的概率是接近的,两者的结构也仅仅只相差一个甲基。
考虑到每个氨基酸i在自然界/细胞中出现的频率f(i)以及数学计算的方便,Dayhoff进一步验证了
\[f(i) * M[j, i] = f(j) * M[i, j]\]并基于这个结论构建了对称PAM1矩阵:
\[PAM[i, j] = log \frac{M[i, j]}{f(i)} = log \frac{f(j) * M[i, j]}{f(j) * f(i)} = log \frac{f(i) * M[j, i]}{f(j) * f(i)} = log \frac{M[j, i]}{f(j)} = PAM[j, i]\]此时,对称PAM矩阵实现了三个优化:
-
对每个突变概率进行了生物学意义上的normalization
-
因为矩阵对称,只需要考虑半个矩阵的分数
-
对蛋白序列每个位点的打分只需要简单相加对称矩阵中的分数
Task 03
根据操作流程的指示,使用距离法、最大简约法和最大似然法进行系统发育树(1000 Bootstrap)的构建,并以PDF或图片的形式保留最终结果。
Y.Mo: 分别使用距离法 (NJ),最大简约法 (MP)和最大似然法 (ML)构建发育树 (Sup.Figure 1-6)。
Task 04
试结合最终结果,解释original tree和Bootstrap consensus tree之间的区别
Y.Mo: Origin tree和Bootstrp consensus tree计算的是同一个数据集的同一个进化模型的不同参数。
Origin tree是在确定数据集和系统发生方法后得出的最优系统树,可以获得系统发生的拓扑结构和支长信息。采用不同的系统发生方法可以获得该方法唯一对应的系统发生origin tree,不同系统发生方法下的节点,支长和结构都有不同。
Bootstrap consensus tree则是根据置进化树置信度计算方法bootsrap重复若干次计算不同次模拟中同一分支模型重复出现的频次,频次越高代表分支结构置信度越高。与origin tree类似,采用不同的置信度计算方法(jack-knifing resampling, permutation)重复截取数据的方式不同,获得的分支结构的重复频次也会各不相同。
Task 05
从构建原理的角度,简单解释不同构建方法所需时间有较大差异的原因
Y.Mo: 分别使用三种不同的方法计算进化树(并且用1000 Bootstrap进行置信度计算),使用的时间ML > > MP > NJ.*
- ML
最大似然法从alignment序列和核酸替代模型出发,分别计算系统发生的拓扑结构和每个位点突变的分数,单从每个突变位点的打分来说,ML的原理是随机设定模型参数获得假设的数据分布,通过先随机参数后缩小范围一步步地逼近数据原分布。这样地穷举法随着序列长度和差异度的增加,计算时间超过了NP问题的标准。[1]
- MP
最大简约法会根据序列差异位点数N定义节点数N,并且列举所有无根树的模型,然后计算所有模型对应的cost (对应site mutation的数量),最后根据所有模型的cost选出最优模型 (最小cost对应最少mutation sites)。 MPd模型的思路与ML相似,但是相比ML,MP不具有每个节点的灵活性,不需要考虑每个节点在进化意义上的变化速率等因素,不需要考虑核算替代模型,虽然相比起ML减少了生物学意义方面的操作空间,但是大大简化了MP的算法和计算耗时。
- NJ
NJ法从星状图出发,同样也是比对后的差异位点数定义节点数N,每个节点都共同连接一个虚拟节点a1形成星状图。首先计算所有位点N形成的Q-matrix (rank = N),距离最短的两个节点,把这两个节点单独分开至一个分支,分支节点a2再连接至初始虚拟节点a1。其次,根据新节点a2和Q-matrix函数计算新的Q-matrix (rank = N-1)。最后,以a2代替此前最近的两个节点和新的Q-matrix (rank = N-1)再找两个距离最近的点计算新的Q-matrix (rank = N-2)。和前两种算法相比,NJ法不需要列举所有可能的模型,无根树的模型唯一确定,极大地省略了无根树模型计算量。
Task 06
以同样的方法分析同样的数据,所产生的树有可能存在不同吗?为什么?
Y.Mo: 数据容量越小,数据差异度越低,系统发生模型越简单,置信度方法取样越少,置信度检验重复次数越少,则最终产生的系统发生树越可能不同。
以其中两个因素举例说明:
-数据容量和差异度低
就目前的实验室建库容量和测序质量来说一般不会出现数据容量小和差异度低的问题,但从系统发生的计算原理来说,数据容量和差异度是系统发生的最基本要求。
数据量小带来的问题是置信度检验时能够重取样的样本容量有限,如果重取样只能有100个不同样本即使重复置信度检验1000次和10000000次都没有区别。
差异度低带来的问题是可能得到数个最优origin tree,置信度检验时同一分支的不同拓扑结构的得分分辨率不高。
-置信度取样数量
比较Bootstrap和Jack-knifing两种方法,前者是从全样本中重新取样,后者是在数据集中划分一刀后取样,两种方法得到的resampling样本容量不同,所计算的分支结构对应频次也不同,给每个拓扑结构的分数也不同,导致最终得出的结构不同。
Abbreviation
ML: Maximum Likelihood
NJ: Neightbor-Join
MP: Maximum Parsimony
References
- Benny Chor, Tamir Tuller, Maximum likelihood of evolutionary trees: hardness and approximation, Bioinformatics, Volume 21, Issue suppl_1, , Pages i97–i106
Supplementary
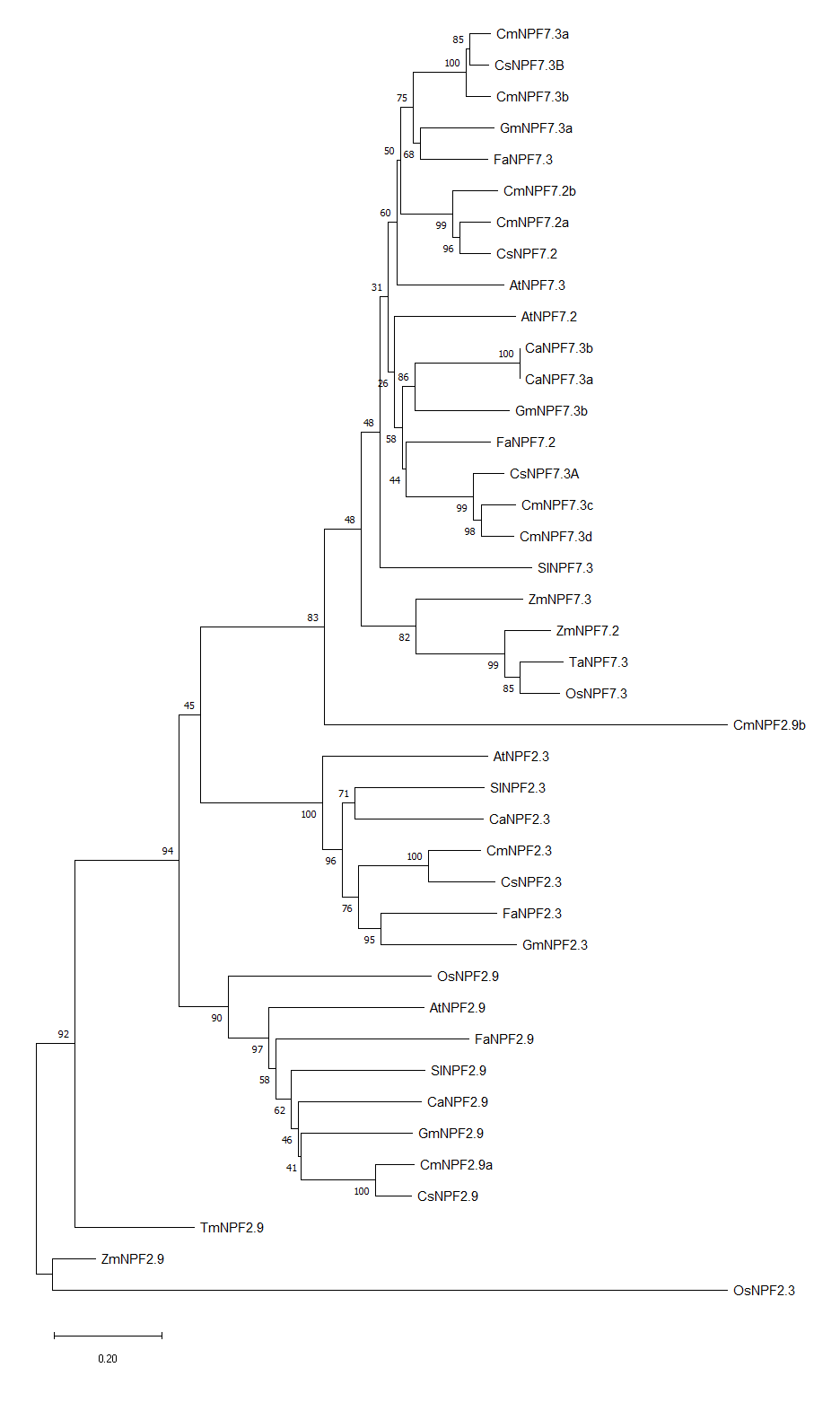
Sup.Figure 1. 使用距离法构建的origin tree

Sup.Figure 2. 使用距离法构建的consensus tree

Sup.Figure 3. 使用最大简约构建的origin tree
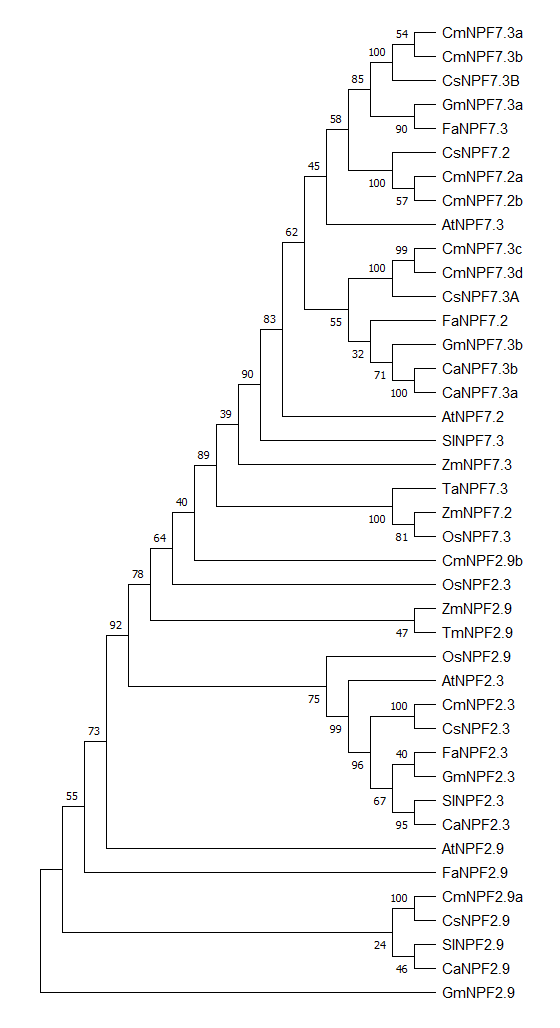
Sup.Figure 4. 使用最大简约法构建的consensus tree
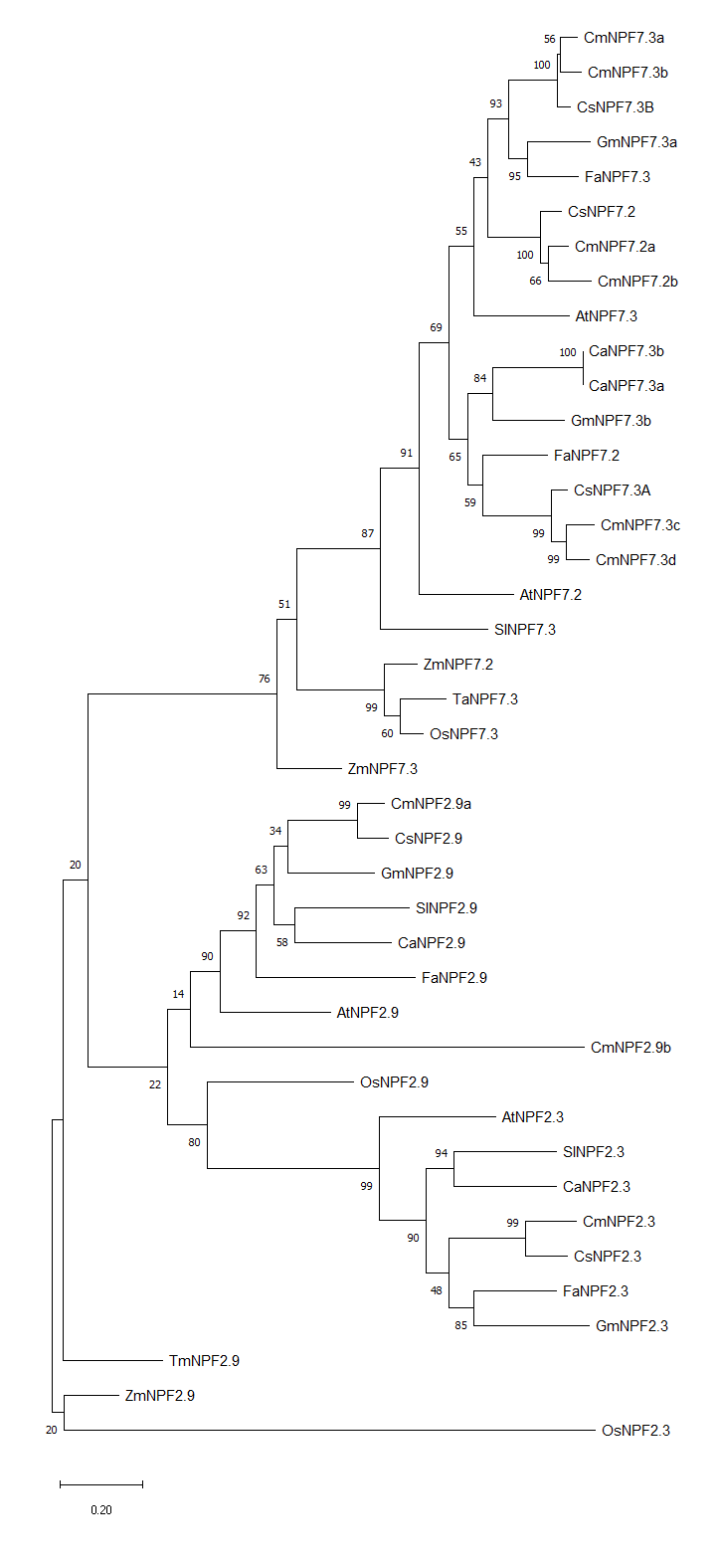
Sup.Figure 5. 使用最大似然法构建的origin tree

Sup.Figure 6. 使用最大简约法构建的consensus tree